Numerische
Simulation der Rissinitiation und Schadensakkumulation von Schienen
FRACTURE MECHANICS
MODELING OF SPALLING IN
THE
ROLLING CONTACT AREA OF WHEEL AND RAIL
DURING A RCF-PROCESS
(in memoriam H.P. Rossmanith)
HERBERT LINSBAUER1, RUDOLF KNASMILLNER2, FRIEDRICH LOIBNEGGER
ROLLING CONTACT AREA OF WHEEL AND RAIL
DURING A RCF-PROCESS
(in memoriam H.P. Rossmanith)
HERBERT LINSBAUER1, RUDOLF KNASMILLNER2, FRIEDRICH LOIBNEGGER
1) TU
Wien, Faculty of Civil Engineering, E222, Karlsplatz 13, A 1040 Wien,
e-mail: herbert.linsbauer@tuwien.ac.at 2) TVFA
GmbH - TU WIEN, Gutheil-Schoder-Gasse 17, 1230 Wien
e-mail: rudolf.knasmillner@tuwien.ac.at
1. Introduction
Increasingly occurring damage incidents on rails of the Vienna subway (Wiener Linien) demanded investigations concerning the assessment of causes and the development of preventive measures in view of triggering effects for macro ruptures. The process of accumulation of damage in the rail-head area is referred to as rolling contact fatigue (Rolling Contact Fatigue RCF) and 'roughly' is characterized by three significant phases:
I) Damage due to material-plasticization on the rail surface
II) Crack formation caused by localized contact pressures
III) Crack propagation extending into rail areas dominated by residual
– temperature and bending stresses

Stage I and stage II are characterized by the so called 'Shake Down Diagram' (Johnson) illustrating 'Elastic Shake Down (ESD) – Plastic Shake Down – and Ratcheting'. We focus here on the state of ESD, assuming an already developed micro crack in the beam like material outbreaks on the surface (head checks, squats) of 'head-hardened (HH) rails of perlitic steel' in the course of RCF processes (Fig. 1)
Fig.
1) Formation of beamlike
material outbreaks (squats)
in the rail head
in the rail head
2. Performance
The starting point for the investigation is the 'in situ' recording of the damage pattern (Fig.1.) and the stress determination in the rail due to the rollover of a Metro train in this section (Fig. 2).
Rolling Contact Fatigue (RCF) crack propagation is described by fracture mechanics based relationships as for example the well known and often used 'Paris Law' and its extensions 'ParisErdogan and Forman' respectively (Fig. 3.)
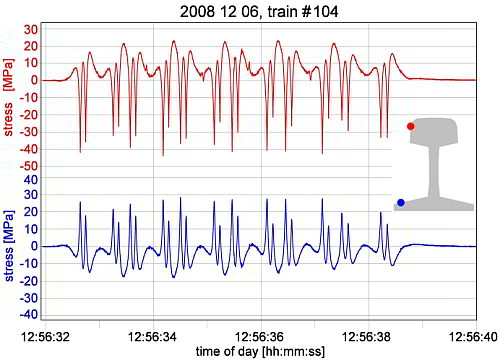
Fig. 2) Axial stresses in the rail head during
rollcontact by a 6-carriage subway train (line
U3), (compressive stress = negativ, tensile stress = positiv; upper curve (red) → side of
rail head, lower curvee (blue) → rail base).
U3), (compressive stress = negativ, tensile stress = positiv; upper curve (red) → side of
rail head, lower curvee (blue) → rail base).
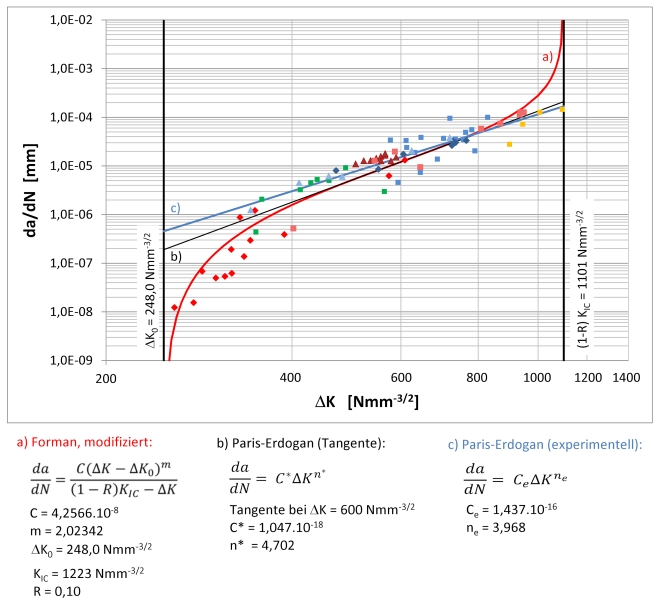
Fig. 3 da/dN versus ΔK diagramm according to ASTM standardized
test specimens from R350HT rail steel
test specimens from R350HT rail steel

Based on these 'special' fatigue fracture mechanics material parameters a FE investigation was carried out for the stepwise surface crack propagation to simulate the life time up to the full break-out of the 'squat–surface crack trough'
(Fig. 4, Fig 5 , Fig. 6).
Fig 4.) Sequence of beam type break-outs
from
ahead hardenend rail surface. Thin section
-m icrophotographic imag
ahead hardenend rail surface. Thin section
-m icrophotographic imag
3. Conclusion
The use of head-hardened,wear-resistant (Heat Treated High Performance Rail 350HT HSH) rails in the Vienna subway system has the risk of cracking (head cheks, squats) in curves and station areas significantly increased, so that special consideration must be focused on optimal rail grinding intervals. As the fatigue crack propagation study (Fig. 6) shows the grinding interval either is aligned on the very conservative Paris-law or by the Erdogan Ratwani relationship, according to instructions of the authorities.
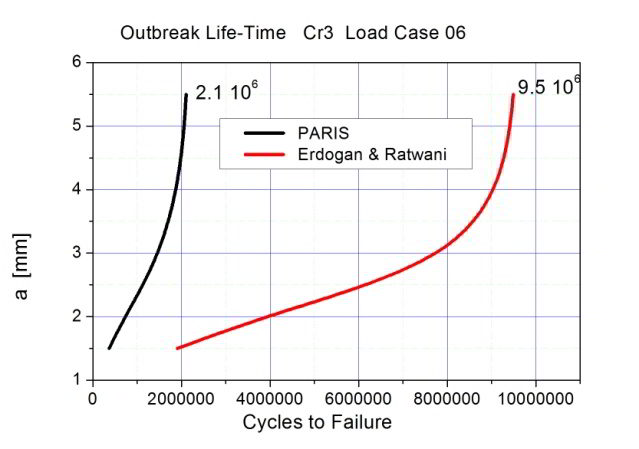
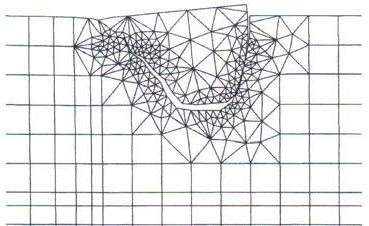
Fig.6.) Fatigue crack growth according to the Fig.5.) FE-FRANC2D - Crack extension study
concepts of Paris and Erdogan-Ratwani
References
[1] A. Ekberg, Rolling contact fatigue of railway wheels , CHARMEC, 1-27
[2] E. Fischmeister, Strukturelles SicherheitsManagement für die Instandhaltung von urbanen
Gleisen, Diss., TU-Wien, 2012
[3] D.I. Fletcher , L. Smith, A. Kapoor, Rail rolling contact fatigue dependence on friction,
predicted using fracture mechanics with a three-dimensional
boundary element model. Engineering Fracture
Mechanics 76 (2009) 2612–2625
[4] D.Y.Jeong, Analytical Modelling of Rail Defects and its Applications to Rail Defect Management,
Uic/Wec Joint Research Project on Rail Defect Management, Jan. 2003, 1-25
[5] J.W. Ringsberg, Life prediction of contact fatigue crack initiation,
International Journal of Fatigue, 23, 2001,575-586
[6] K.Dang Van, M.H. Maitournam ,Z. Moumni F. Roger, A comprehensive approach for modeling
fatigue and fracture of rails, Engineering Fracture Mechanics 76 (2009) 2626–2636
[7] U. Zerbst, R. Lundén, K.-O. Ede, R.A. Smith, Introduction to the damage tolerance behaviour of
railway rails–a review, Engineering Fracture Mechanics 76 (2009) 2563–2601
[1] A. Ekberg, Rolling contact fatigue of railway wheels , CHARMEC, 1-27
[2] E. Fischmeister, Strukturelles SicherheitsManagement für die Instandhaltung von urbanen
Gleisen, Diss., TU-Wien, 2012
[3] D.I. Fletcher , L. Smith, A. Kapoor, Rail rolling contact fatigue dependence on friction,
predicted using fracture mechanics with a three-dimensional
boundary element model. Engineering Fracture
Mechanics 76 (2009) 2612–2625
[4] D.Y.Jeong, Analytical Modelling of Rail Defects and its Applications to Rail Defect Management,
Uic/Wec Joint Research Project on Rail Defect Management, Jan. 2003, 1-25
[5] J.W. Ringsberg, Life prediction of contact fatigue crack initiation,
International Journal of Fatigue, 23, 2001,575-586
[6] K.Dang Van, M.H. Maitournam ,Z. Moumni F. Roger, A comprehensive approach for modeling
fatigue and fracture of rails, Engineering Fracture Mechanics 76 (2009) 2626–2636
[7] U. Zerbst, R. Lundén, K.-O. Ede, R.A. Smith, Introduction to the damage tolerance behaviour of
railway rails–a review, Engineering Fracture Mechanics 76 (2009) 2563–2601
=============================================================================
Parallel-Untersuchungen Promper:
Als Vergleich wird die Schienen Rad Konstruktion einer Triebwagenkostruktion untersucht:
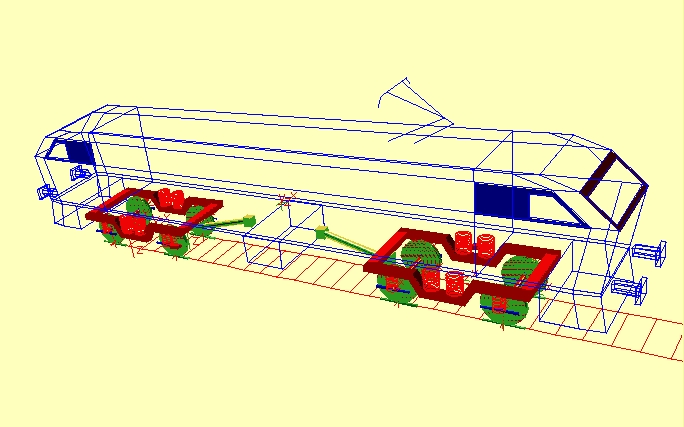
Die Vibrationen der Kräfte können wie nachfolgend beschrieben werden im Kontakt Schiene Rad beschrieben werden:
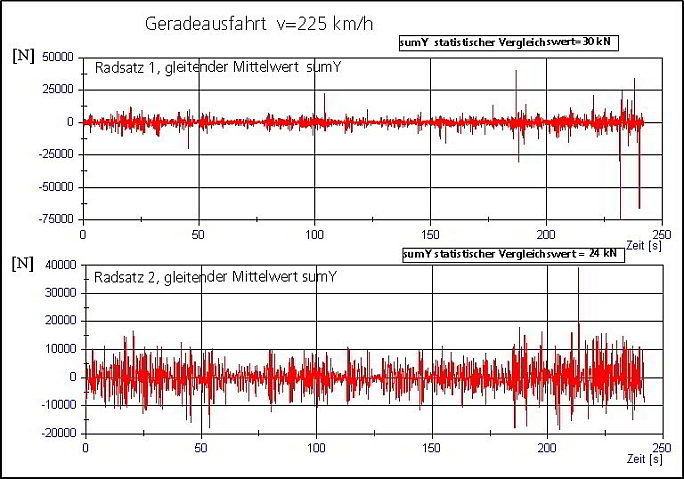
Diese Untersuchung wurde mittels CODE-ASTER geführt. Es zeigen sich sehr schöne TRESCA-Maxima in Richtung des Schubes versetzt.
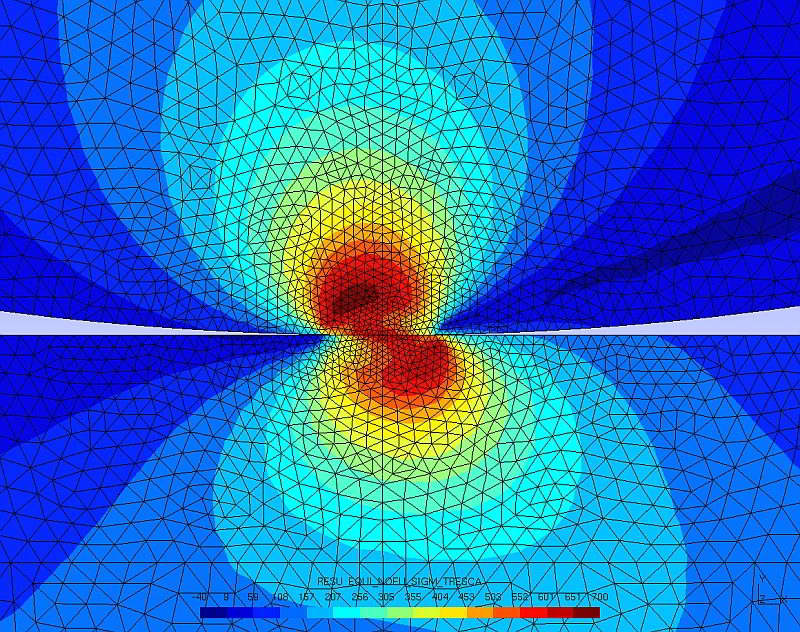
Die eigentliche Untersuchung wurde später mittels 3D Modell durchgeführt:
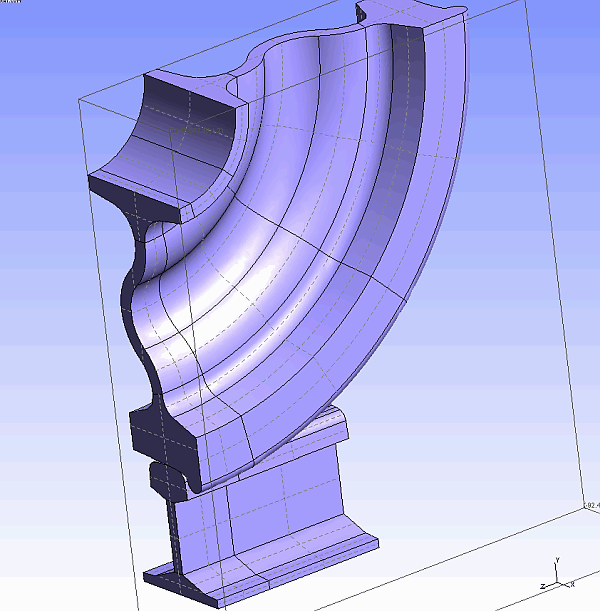


Nachfolgend wird noch dass ASTK - Chemata zur Berechnung des räumlichen Kontaktes angefügt:
CODE-ASTER BERECHNUNG:
======================== # MODIF DATE 04/04/2007 AUTEUR ABBAS M.ABBAS
#
# TITRE CONTACT MULTICORPS ELASTIQUES
# CONFIGURATION MANAGEMENT OF EDF VERSION
# ======================================================================
# COPYRIGHT (C) 1991 - 2004 EDF R&D WWW.CODE-ASTER.ORG
# THIS PROGRAM IS FREE SOFTWARE; YOU CAN REDISTRIBUTE IT AND/OR MODIFY
# IT UNDER THE TERMS OF THE GNU GENERAL PUBLIC LICENSE AS PUBLISHED BY
# THE FREE SOFTWARE FOUNDATION; EITHER VERSION 2 OF THE LICENSE, OR
# (AT YOUR OPTION) ANY LATER VERSION.
#
# THIS PROGRAM IS DISTRIBUTED IN THE HOPE THAT IT WILL BE USEFUL, BUT
# WITHOUT ANY WARRANTY; WITHOUT EVEN THE IMPLIED WARRANTY OF
# MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. SEE THE GNU
# GENERAL PUBLIC LICENSE FOR MORE DETAILS.
#
# YOU SHOULD HAVE RECEIVED A COPY OF THE GNU GENERAL PUBLIC LICENSE
# ALONG WITH THIS PROGRAM; IF NOT, WRITE TO EDF R&D CODE_ASTER,
# 1 AVENUE DU GENERAL DE GAULLE, 92141 CLAMART CEDEX, FRANCE.
# ======================================================================
#
# REFERENCE : CALCULS AVEC ABAQUS, SYSTUS, SAMCEF
#########################################
# METHODE DE CONTACT : LAGRANGIEN
# METHODE METAL : ROUSSELIN
# =======================================================
# Das Beispiel SSNA102D wird als Grundlage der Berechnung des Kontaktes
# verwendet
# RAD Schiene Ganzes System
# =======================================================
#DEBUT(CODE=_F(NOM='SSNA102D',
# NIV_PUB_WEB='INTERNET',),);
DEBUT(CODE=_F(NOM='RAD_SCHIENE_3D_ROUSS',
NIV_PUB_WEB='INTERNET',),);
# --------------------------------------------------------------------
# LECTURE DU MAILLAGE ET CREATION DE GROUPES DE NOEUDS
# --------------------------------------------------------------------
MAIL=LIRE_MAILLAGE(UNITE=19,
FORMAT='MED',
VERI_MAIL=_F(VERIF='OUI',),
INFO=1,);
MAIL=DEFI_GROUP(reuse =MAIL,
MAILLAGE=MAIL,
CREA_GROUP_NO=(_F(GROUP_MA='SfSymRd',
NOM='NdSymRd',),
_F(GROUP_MA='SfSymSc',
NOM='NdSymSc',),
_F(GROUP_MA='NdLoadA',
NOM='NDLoadA',),
_F(GROUP_MA='LnSuppR',
NOM='NdSuppR',),
_F(GROUP_MA='LnLoadA',
NOM='NdLinLoA',),
_F(GROUP_MA='SfSpSch',
NOM='NdSpSch',),),);
#
# --------------------------------------------------------------------
# MODELISATION 3D
# --------------------------------------------------------------------
MOD=AFFE_MODELE(MAILLAGE=MAIL,
AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',
MODELISATION='3D',),);
# ------------------------------------------------------------------------
# !!!!! IMPORTANT POUR CONTACT AREAL !!!!!
# ------------------------------------------------------------------------
MAIL=MODI_MAILLAGE(reuse =MAIL,
MAILLAGE=MAIL,
ORIE_PEAU_3D=_F(GROUP_MA=('SfConSch','SfConRd',),),
INFO=1,);
#
# --------------------------------------------------------------------
# DEFINITION ET AFFECTATION D'UN MATERIAU ELASTIQUE
# --------------------------------------------------------------------
# ....... kN/cm²
# In N/mm2 Rad_Modul gleich dem Kugel Modul gesetzt (Faktor 1.0) !!!!
EM = 210000.0;
ER = EM;
ER = (EM / 1.0);
ESK = EM;
ESSt = EM;
ESF = EM;
#
# --------------------------------------------------------------------
# DEFINITION D'UN MATERIAU ROUSSELIER
# --------------------------------------------------------------------
# Hier habe ich dre gefundene Kurven eingetragen
ECR00=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,273.0,
0.03,519.58,
0.04,580.94,
0.05,633.48,
0.07,721.82,
0.1,828.96,
0.15,970.19,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
# Fuer die Konvergenz habe ich die Spannungswerte einfach mit 2 Multipliziert !!!!
# ECR02
ECR02=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,546.0,
0.03,1021.90,
0.04,1161.88,
0.05,1266.96,
0.07,1443.64,
0.1,1657.92,
0.15,1940.38,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
# Fuer die Konvergenz habe ich die Spannungswerte einfach mit 4 Multipliziert !!!!
ECRa=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,1092.0,
0.03,2078.3,
0.04,2323.76,
0.05,2533.92,
0.07,2887.28,
0.1,3315.84,
0.15,3880.76,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
# Multiplizieren der Funktion zur genauen Anpassung !!!
ECR=CALC_FONCTION(COMB=_F(FONCTION=ECRa,
COEF=1.00000,),);
ECR1=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,222.0,
0.00338,272.0,
0.03,519.58,
0.04,580.94,
0.05,633.48,
0.07,721.82,
0.1,828.96,
0.15,970.19,
0.2,1084.75,
0.3,1269.57,
0.4,1419.48,
0.5,1547.86,
0.7,1763.72,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
ECR2=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,350.00,
0.02,400.00,
0.10,450.00,
0.15,470.00,
0.20,430.00,
0.25,380.00,
),INTERPOL='LIN',PROL_DROITE='LINEAIRE',PROL_GAUCHE='EXCLU',);
# NON LIMITE
ECR9=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,90000.00,
0.15,180000.00,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
#
#D_T=DEFI_CONSTANTE(VALE = 2.0)
# KONSTANTE ETWA AUS sfb02-08.pdf
# !!!! Hier ist jedoch viel anzupassen !!!!
D_T = 2.0;
S_T = 590.0;
F0_T = 0.0001;
# ~~~~ Steel Def TRACTION
IMPR_FONCTION(FORMAT='XMGRACE',
UNITE=29,
COURBE=(_F(FONCTION=ECR,),
_F(FONCTION=ECR1,),
_F(FONCTION=ECR00,),
_F(FONCTION=ECR02,),
_F(FONCTION=ECR2,),),);
# ~~~~
#ERad=DEFI_MATERIAU(ELAS=_F(E=ER,
# NU=0.3,
# RHO=7.8e-3,),);
ERad=DEFI_MATERIAU(ELAS=_F(E=ER,
NU=0.3,),
TRACTION=_F(SIGM=ECR9,),
ROUSSELIER=_F(D=D_T,
SIGM_1=S_T,
PORO_INIT=F0_T,
PORO_CRIT=1.0,
PORO_ACCE=1.0,
D_SIGM_EPSI_NORM=1.0,),);
ESchK=DEFI_MATERIAU(ELAS=_F(E=ESK,
NU=0.3,),
TRACTION=_F(SIGM=ECR,),
ROUSSELIER=_F(D=D_T,
SIGM_1=S_T,
PORO_INIT=F0_T,
PORO_CRIT=1.0,
PORO_ACCE=1.0,
D_SIGM_EPSI_NORM=1.0,),);
#ESchSt=DEFI_MATERIAU(ELAS=_F(E=ESSt,
# NU=0.3,
# RHO=7.8e-3,),);
ESchSt=DEFI_MATERIAU(ELAS=_F(E=ESSt,
NU=0.3,),
TRACTION=_F(SIGM=ECR,),
ROUSSELIER=_F(D=D_T,
SIGM_1=S_T,
PORO_INIT=F0_T,
PORO_CRIT=1.0,
PORO_ACCE=1.0,
D_SIGM_EPSI_NORM=1.0,),);
#ESchF=DEFI_MATERIAU(ELAS=_F(E=ESF,
# NU=0.3,
# RHO=7.8e-3,),);
ESchF=DEFI_MATERIAU(ELAS=_F(E=ESF,
NU=0.3,),
TRACTION=_F(SIGM=ECR9,),
ROUSSELIER=_F(D=D_T,
SIGM_1=S_T,
PORO_INIT=F0_T,
PORO_CRIT=1.0,
PORO_ACCE=1.0,
D_SIGM_EPSI_NORM=1.0,),);
#
CHMAT=AFFE_MATERIAU(MAILLAGE=MAIL,
AFFE=(_F(GROUP_MA='VlRad',
MATER=ERad,),
_F(GROUP_MA='VlSchi',
MATER=ESchK,),),);
#
# --------------------------------------------------------------------
# ENCASTREMENT DE LA LIGNE SchiLaNd
# --------------------------------------------------------------------
BLOQ=AFFE_CHAR_MECA(MODELE=MOD,
DDL_IMPO=(_F(GROUP_NO=('NdSymSc','NdSymRd',),
DZ=0.0,),
_F(GROUP_NO=('NDLoadA','NdSpSch',),
DX=0.0,
DZ=0.0,),
_F(GROUP_NO='NdSuppR',
DX=0.0,
DY=0.0,
DZ=0.0,),
_F(GROUP_NO='NdLinLoA',
DX=0.0,
DZ=0.0,),),
LIAISON_UNIF=_F(GROUP_NO='NdLinLoA',
DDL='DY',),);
#
# --------------------------------------------------------------------
# DEPLACEMENT IMPOSE SUR LA LIGNE RadNdLd
# --------------------------------------------------------------------
# Belastung 50 kN / cm Schienenkopf also bei 4 cm ... 400 kN = 40 to
# Schub 15 kN; Exzentrizitaet = 46 cm da Radius = 460 mm
# Normalkraft der Kugel wird auf 11.0 mm verteilt; jedoch aus Vergleichsrechnung
# mit dem Faktor 3.0 multipliziert
NormalK = 25000.0;
NormalK = NormalK;
SchubF = 0.2;
Schub = (NormalK * SchubF);
Moment = (Schub * 46.0);
LinDif = 2.0;
N1 = (Moment / (2.0 * LinDif));
# =======================================
AchDr=-(0.3939)
# =======================================
#
DEPL=AFFE_CHAR_MECA(MODELE=MOD,
DDL_IMPO=_F(GROUP_NO='NDLoadA',
DY=-0.3939,),);
#
# --------------------------------------------------------------------
# SUPPRESSION DES MOUVEMENTS DE CORPS RIGIDE DES DEUX SPHERES
# --------------------------------------------------------------------
#LIAI=AFFE_CHAR_MECA(MODELE=MOD,
# LIAISON_GROUP=_F(GROUP_NO_1='NdConR',
# GROUP_NO_2='NdConS',
# DDL_1='DY',
# COEF_MULT_1=1.0,
# DDL_2='DY',
# COEF_MULT_2=-1.0,
# COEF_IMPO=0.0,),);
# --------------------------------------------------------------------
# CONTACT UNILATERAL : FORMULATION MAITRE-ESCLAVE (3 ZONES)
# --------------------------------------------------------------------
# Berechnung nur fuer den Kontakt; ohne Reibung wurde COULOMB=0.01 gesetzt
CONT=AFFE_CHAR_MECA(MODELE=MOD,
CONTACT=_F(APPARIEMENT='MAIT_ESCL',
METHODE='LAGRANGIEN',
GROUP_MA_MAIT='SfConSch',
GROUP_MA_ESCL='SfConRd',),
INFO=1,);
# Berechnung Kontakt mit Versagen
#CONT=AFFE_CHAR_MECA(MODELE=MOD,
# CONTACT=_F(METHODE='CONTINUE',
# GROUP_MA_MAIT='EdLIAM0',
# GROUP_MA_ESCL='EdLIAE0',
# COEF_REGU_CONT=100.0,
# ITER_GEOM_MAXI=10,
# ITER_CONT_MAXI=4,
# CONTACT_INIT='OUI',
# FROTTEMENT='COULOMB',
# COEF_REGU_FROT=90.0,
# COULOMB=0.30,
# ITER_FROT_MAXI=10,),
# INFO=2,);
#
# --------------------------------------------------------------------
# DECOUPAGE EN INCREMENTS DE CHARGE (1 EN ELASTICITE)
# ET RAMPE MULTIPLICATRICE POUR LE DEPLACEMENT IMPOSE
# --------------------------------------------------------------------
FONC=DEFI_FONCTION(NOM_PARA='INST',VALE=(0.,0.,
1.,1.,
),);
#
LoadStp = 4;
LoadFc = 1.0;
LINST=DEFI_LIST_REEL(DEBUT=0.0,
INTERVALLE=_F(JUSQU_A=LoadFc,
NOMBRE=LoadStp,),);
#
# --------------------------------------------------------------------
# CALCUL NON LINEAIRE
# --------------------------------------------------------------------
RESU=STAT_NON_LINE(MODELE=MOD,
CHAM_MATER=CHMAT,
EXCIT=(_F(CHARGE=BLOQ,),
_F(CHARGE=DEPL,
FONC_MULT=FONC,),
_F(CHARGE=CONT,),),
COMP_INCR=(_F(RELATION='ELAS',
DEFORMATION='PETIT_REAC',
GROUP_MA='VlSchi',),
_F(RELATION='ELAS',
DEFORMATION='PETIT_REAC',
GROUP_MA='VlRad',),),
INCREMENT=_F(LIST_INST=LINST,
SUBD_METHODE='UNIFORME',
SUBD_PAS=6,
SUBD_NIVEAU=5,
SUBD_PAS_MINI=1.0E-8,),
NEWTON=_F(MATRICE='TANGENTE',),
CONVERGENCE=_F(RESI_GLOB_RELA=1.0E-6,
ITER_GLOB_MAXI=300,),
SOLVEUR=_F(METHODE='MULT_FRONT',
SYME='OUI',),
INFO=1,);
#
# --------------------------------------------------------------------
# CALCUL DES CONTRAINTES AUX NOEUDS
# --------------------------------------------------------------------
#
RESU=CALC_ELEM(reuse =RESU,
MODELE=MOD,
CHAM_MATER=CHMAT,
RESULTAT=RESU,
OPTION=('SIEF_ELNO_ELGA','VARI_ELNO_ELGA','EQUI_ELNO_SIGM',),);
RESU=CALC_NO(reuse =RESU,
RESULTAT=RESU,
OPTION=('SIEF_NOEU_ELGA','VARI_NOEU_ELGA','EQUI_NOEU_SIGM',),);
RESU=CALC_NO(reuse =RESU,
RESULTAT=RESU,
OPTION='FORC_NODA',
MODELE=MOD,
CHAM_MATER=CHMAT,);
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Compute reaction force on the imposed displacement surface "DEPL"
# Caution : force expressed in n/radian
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
TAB_FORC=POST_RELEVE_T(ACTION=_F(OPERATION='EXTRACTION',
INTITULE='FORCE',
RESULTAT=RESU,
NOM_CHAM='FORC_NODA',
TOUT_ORDRE='OUI',
GROUP_NO='NDLoadA',
RESULTANTE='DY',),);
# Turn the table TAB_FORC into a function
FF=RECU_FONCTION(TABLE=TAB_FORC,
PARA_X='INST',
PARA_Y='DY',);
# Multiply the function by -1.
FY=CALC_FONCTION(COMB=_F(FONCTION=FF,
COEF=-1.,),);
# Create a function out of the displacement on node "Point"
DD=RECU_FONCTION(RESULTAT=RESU,
TOUT_ORDRE='OUI',
NOM_CHAM='DEPL',
NOM_CMP='DY',
GROUP_NO='NDLoadA',);
# Multiply the function by -1.
DY=CALC_FONCTION(COMB=_F(FONCTION=DD,
COEF=-1.,),);
# Print a nice postscript curve in 38 logic unit
IMPR_FONCTION(FORMAT='XMGRACE',
UNITE=28,
COURBE=_F(FONC_X=DY,
FONC_Y=FY,
COULEUR=2,),
SOUS_TITRE='Force (N/mm)',
LEGENDE_X='Depth (mm)',);
# Print text function in 39 logic unit
#IMPR_FONCTION(FORMAT='TABLEAU',
# COURBE=_F(FONC_X=DY,
# FONC_Y=FY,),
# UNITE=39,);
#
# --------------------------------------------------------------------
# CALCUL DES FORCES NODALES ET DES REACTIONS NODALES
# --------------------------------------------------------------------
#RESU=CALC_NO(reuse =RESU,
# RESULTAT=RESU,
# OPTION='REAC_NODA',
# MODELE=MOD,
# EXCIT=(_F(CHARGE=BLOQ,),
# _F(CHARGE=DEPL,
# FONC_MULT=FONC,),
# _F(CHARGE=LIAI,),
# _F(CHARGE=CONT,),),);
#
# =====================================================================
# Pro 21.01.09 GMSH OUTPUT
# FEHLER GMSH OUTPUT ENTFERNT DURCH EINSETZEN DER TERME FUER COMPOSANTES
# NOM_CMP=('SIXX','SIYY','SIXY',),),
# =====================================================================
IMPR_RESU(MODELE=MOD,
FORMAT='GMSH',
UNITE=81,
RESU=(_F(MAILLAGE=MAIL,
RESULTAT=RESU,
NOM_CHAM='DEPL',
NUME_ORDRE=4,),
_F(RESULTAT=RESU,
NOM_CHAM='SIEF_NOEU_ELGA',
NUME_ORDRE=4,
NOM_CMP=('SIXX','SIYY','SIZZ',),),
_F(RESULTAT=RESU,
NOM_CHAM='VARI_NOEU_ELGA',
NUME_ORDRE=4,),
_F(RESULTAT=RESU,
NOM_CHAM='EQUI_NOEU_SIGM',
NUME_ORDRE=4,
NOM_CMP=('PRIN_1','PRIN_2','PRIN_3','TRESCA',),),
_F(RESULTAT=RESU,
NOM_CHAM='VALE_CONT',
NUME_ORDRE=4,
NOM_CMP='RN',),),);
#
#IMPR_RESU(FORMAT='MED',
# UNITE=80,
# RESU=_F(MAILLAGE=MAIL,
# RESULTAT=RESU,
# NOM_CHAM=('DEPL','SIEF_NOEU_ELGA','VARI_NOEU_ELGA',),),);
# ===================
# STANLEY();
# ===================
# =====================================================================
FIN();
#
======================== # MODIF DATE 04/04/2007 AUTEUR ABBAS M.ABBAS
#
# TITRE CONTACT MULTICORPS ELASTIQUES
# CONFIGURATION MANAGEMENT OF EDF VERSION
# ======================================================================
# COPYRIGHT (C) 1991 - 2004 EDF R&D WWW.CODE-ASTER.ORG
# THIS PROGRAM IS FREE SOFTWARE; YOU CAN REDISTRIBUTE IT AND/OR MODIFY
# IT UNDER THE TERMS OF THE GNU GENERAL PUBLIC LICENSE AS PUBLISHED BY
# THE FREE SOFTWARE FOUNDATION; EITHER VERSION 2 OF THE LICENSE, OR
# (AT YOUR OPTION) ANY LATER VERSION.
#
# THIS PROGRAM IS DISTRIBUTED IN THE HOPE THAT IT WILL BE USEFUL, BUT
# WITHOUT ANY WARRANTY; WITHOUT EVEN THE IMPLIED WARRANTY OF
# MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. SEE THE GNU
# GENERAL PUBLIC LICENSE FOR MORE DETAILS.
#
# YOU SHOULD HAVE RECEIVED A COPY OF THE GNU GENERAL PUBLIC LICENSE
# ALONG WITH THIS PROGRAM; IF NOT, WRITE TO EDF R&D CODE_ASTER,
# 1 AVENUE DU GENERAL DE GAULLE, 92141 CLAMART CEDEX, FRANCE.
# ======================================================================
#
# REFERENCE : CALCULS AVEC ABAQUS, SYSTUS, SAMCEF
#########################################
# METHODE DE CONTACT : LAGRANGIEN
# METHODE METAL : ROUSSELIN
# =======================================================
# Das Beispiel SSNA102D wird als Grundlage der Berechnung des Kontaktes
# verwendet
# RAD Schiene Ganzes System
# =======================================================
#DEBUT(CODE=_F(NOM='SSNA102D',
# NIV_PUB_WEB='INTERNET',),);
DEBUT(CODE=_F(NOM='RAD_SCHIENE_3D_ROUSS',
NIV_PUB_WEB='INTERNET',),);
# --------------------------------------------------------------------
# LECTURE DU MAILLAGE ET CREATION DE GROUPES DE NOEUDS
# --------------------------------------------------------------------
MAIL=LIRE_MAILLAGE(UNITE=19,
FORMAT='MED',
VERI_MAIL=_F(VERIF='OUI',),
INFO=1,);
MAIL=DEFI_GROUP(reuse =MAIL,
MAILLAGE=MAIL,
CREA_GROUP_NO=(_F(GROUP_MA='SfSymRd',
NOM='NdSymRd',),
_F(GROUP_MA='SfSymSc',
NOM='NdSymSc',),
_F(GROUP_MA='NdLoadA',
NOM='NDLoadA',),
_F(GROUP_MA='LnSuppR',
NOM='NdSuppR',),
_F(GROUP_MA='LnLoadA',
NOM='NdLinLoA',),
_F(GROUP_MA='SfSpSch',
NOM='NdSpSch',),),);
#
# --------------------------------------------------------------------
# MODELISATION 3D
# --------------------------------------------------------------------
MOD=AFFE_MODELE(MAILLAGE=MAIL,
AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',
MODELISATION='3D',),);
# ------------------------------------------------------------------------
# !!!!! IMPORTANT POUR CONTACT AREAL !!!!!
# ------------------------------------------------------------------------
MAIL=MODI_MAILLAGE(reuse =MAIL,
MAILLAGE=MAIL,
ORIE_PEAU_3D=_F(GROUP_MA=('SfConSch','SfConRd',),),
INFO=1,);
#
# --------------------------------------------------------------------
# DEFINITION ET AFFECTATION D'UN MATERIAU ELASTIQUE
# --------------------------------------------------------------------
# ....... kN/cm²
# In N/mm2 Rad_Modul gleich dem Kugel Modul gesetzt (Faktor 1.0) !!!!
EM = 210000.0;
ER = EM;
ER = (EM / 1.0);
ESK = EM;
ESSt = EM;
ESF = EM;
#
# --------------------------------------------------------------------
# DEFINITION D'UN MATERIAU ROUSSELIER
# --------------------------------------------------------------------
# Hier habe ich dre gefundene Kurven eingetragen
ECR00=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,273.0,
0.03,519.58,
0.04,580.94,
0.05,633.48,
0.07,721.82,
0.1,828.96,
0.15,970.19,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
# Fuer die Konvergenz habe ich die Spannungswerte einfach mit 2 Multipliziert !!!!
# ECR02
ECR02=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,546.0,
0.03,1021.90,
0.04,1161.88,
0.05,1266.96,
0.07,1443.64,
0.1,1657.92,
0.15,1940.38,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
# Fuer die Konvergenz habe ich die Spannungswerte einfach mit 4 Multipliziert !!!!
ECRa=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,1092.0,
0.03,2078.3,
0.04,2323.76,
0.05,2533.92,
0.07,2887.28,
0.1,3315.84,
0.15,3880.76,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
# Multiplizieren der Funktion zur genauen Anpassung !!!
ECR=CALC_FONCTION(COMB=_F(FONCTION=ECRa,
COEF=1.00000,),);
ECR1=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,222.0,
0.00338,272.0,
0.03,519.58,
0.04,580.94,
0.05,633.48,
0.07,721.82,
0.1,828.96,
0.15,970.19,
0.2,1084.75,
0.3,1269.57,
0.4,1419.48,
0.5,1547.86,
0.7,1763.72,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
ECR2=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,350.00,
0.02,400.00,
0.10,450.00,
0.15,470.00,
0.20,430.00,
0.25,380.00,
),INTERPOL='LIN',PROL_DROITE='LINEAIRE',PROL_GAUCHE='EXCLU',);
# NON LIMITE
ECR9=DEFI_FONCTION(NOM_PARA='EPSI',VALE=(0.0001,90000.00,
0.15,180000.00,
),PROL_DROITE='LINEAIRE',PROL_GAUCHE='LINEAIRE',);
#
#D_T=DEFI_CONSTANTE(VALE = 2.0)
# KONSTANTE ETWA AUS sfb02-08.pdf
# !!!! Hier ist jedoch viel anzupassen !!!!
D_T = 2.0;
S_T = 590.0;
F0_T = 0.0001;
# ~~~~ Steel Def TRACTION
IMPR_FONCTION(FORMAT='XMGRACE',
UNITE=29,
COURBE=(_F(FONCTION=ECR,),
_F(FONCTION=ECR1,),
_F(FONCTION=ECR00,),
_F(FONCTION=ECR02,),
_F(FONCTION=ECR2,),),);
# ~~~~
#ERad=DEFI_MATERIAU(ELAS=_F(E=ER,
# NU=0.3,
# RHO=7.8e-3,),);
ERad=DEFI_MATERIAU(ELAS=_F(E=ER,
NU=0.3,),
TRACTION=_F(SIGM=ECR9,),
ROUSSELIER=_F(D=D_T,
SIGM_1=S_T,
PORO_INIT=F0_T,
PORO_CRIT=1.0,
PORO_ACCE=1.0,
D_SIGM_EPSI_NORM=1.0,),);
ESchK=DEFI_MATERIAU(ELAS=_F(E=ESK,
NU=0.3,),
TRACTION=_F(SIGM=ECR,),
ROUSSELIER=_F(D=D_T,
SIGM_1=S_T,
PORO_INIT=F0_T,
PORO_CRIT=1.0,
PORO_ACCE=1.0,
D_SIGM_EPSI_NORM=1.0,),);
#ESchSt=DEFI_MATERIAU(ELAS=_F(E=ESSt,
# NU=0.3,
# RHO=7.8e-3,),);
ESchSt=DEFI_MATERIAU(ELAS=_F(E=ESSt,
NU=0.3,),
TRACTION=_F(SIGM=ECR,),
ROUSSELIER=_F(D=D_T,
SIGM_1=S_T,
PORO_INIT=F0_T,
PORO_CRIT=1.0,
PORO_ACCE=1.0,
D_SIGM_EPSI_NORM=1.0,),);
#ESchF=DEFI_MATERIAU(ELAS=_F(E=ESF,
# NU=0.3,
# RHO=7.8e-3,),);
ESchF=DEFI_MATERIAU(ELAS=_F(E=ESF,
NU=0.3,),
TRACTION=_F(SIGM=ECR9,),
ROUSSELIER=_F(D=D_T,
SIGM_1=S_T,
PORO_INIT=F0_T,
PORO_CRIT=1.0,
PORO_ACCE=1.0,
D_SIGM_EPSI_NORM=1.0,),);
#
CHMAT=AFFE_MATERIAU(MAILLAGE=MAIL,
AFFE=(_F(GROUP_MA='VlRad',
MATER=ERad,),
_F(GROUP_MA='VlSchi',
MATER=ESchK,),),);
#
# --------------------------------------------------------------------
# ENCASTREMENT DE LA LIGNE SchiLaNd
# --------------------------------------------------------------------
BLOQ=AFFE_CHAR_MECA(MODELE=MOD,
DDL_IMPO=(_F(GROUP_NO=('NdSymSc','NdSymRd',),
DZ=0.0,),
_F(GROUP_NO=('NDLoadA','NdSpSch',),
DX=0.0,
DZ=0.0,),
_F(GROUP_NO='NdSuppR',
DX=0.0,
DY=0.0,
DZ=0.0,),
_F(GROUP_NO='NdLinLoA',
DX=0.0,
DZ=0.0,),),
LIAISON_UNIF=_F(GROUP_NO='NdLinLoA',
DDL='DY',),);
#
# --------------------------------------------------------------------
# DEPLACEMENT IMPOSE SUR LA LIGNE RadNdLd
# --------------------------------------------------------------------
# Belastung 50 kN / cm Schienenkopf also bei 4 cm ... 400 kN = 40 to
# Schub 15 kN; Exzentrizitaet = 46 cm da Radius = 460 mm
# Normalkraft der Kugel wird auf 11.0 mm verteilt; jedoch aus Vergleichsrechnung
# mit dem Faktor 3.0 multipliziert
NormalK = 25000.0;
NormalK = NormalK;
SchubF = 0.2;
Schub = (NormalK * SchubF);
Moment = (Schub * 46.0);
LinDif = 2.0;
N1 = (Moment / (2.0 * LinDif));
# =======================================
AchDr=-(0.3939)
# =======================================
#
DEPL=AFFE_CHAR_MECA(MODELE=MOD,
DDL_IMPO=_F(GROUP_NO='NDLoadA',
DY=-0.3939,),);
#
# --------------------------------------------------------------------
# SUPPRESSION DES MOUVEMENTS DE CORPS RIGIDE DES DEUX SPHERES
# --------------------------------------------------------------------
#LIAI=AFFE_CHAR_MECA(MODELE=MOD,
# LIAISON_GROUP=_F(GROUP_NO_1='NdConR',
# GROUP_NO_2='NdConS',
# DDL_1='DY',
# COEF_MULT_1=1.0,
# DDL_2='DY',
# COEF_MULT_2=-1.0,
# COEF_IMPO=0.0,),);
# --------------------------------------------------------------------
# CONTACT UNILATERAL : FORMULATION MAITRE-ESCLAVE (3 ZONES)
# --------------------------------------------------------------------
# Berechnung nur fuer den Kontakt; ohne Reibung wurde COULOMB=0.01 gesetzt
CONT=AFFE_CHAR_MECA(MODELE=MOD,
CONTACT=_F(APPARIEMENT='MAIT_ESCL',
METHODE='LAGRANGIEN',
GROUP_MA_MAIT='SfConSch',
GROUP_MA_ESCL='SfConRd',),
INFO=1,);
# Berechnung Kontakt mit Versagen
#CONT=AFFE_CHAR_MECA(MODELE=MOD,
# CONTACT=_F(METHODE='CONTINUE',
# GROUP_MA_MAIT='EdLIAM0',
# GROUP_MA_ESCL='EdLIAE0',
# COEF_REGU_CONT=100.0,
# ITER_GEOM_MAXI=10,
# ITER_CONT_MAXI=4,
# CONTACT_INIT='OUI',
# FROTTEMENT='COULOMB',
# COEF_REGU_FROT=90.0,
# COULOMB=0.30,
# ITER_FROT_MAXI=10,),
# INFO=2,);
#
# --------------------------------------------------------------------
# DECOUPAGE EN INCREMENTS DE CHARGE (1 EN ELASTICITE)
# ET RAMPE MULTIPLICATRICE POUR LE DEPLACEMENT IMPOSE
# --------------------------------------------------------------------
FONC=DEFI_FONCTION(NOM_PARA='INST',VALE=(0.,0.,
1.,1.,
),);
#
LoadStp = 4;
LoadFc = 1.0;
LINST=DEFI_LIST_REEL(DEBUT=0.0,
INTERVALLE=_F(JUSQU_A=LoadFc,
NOMBRE=LoadStp,),);
#
# --------------------------------------------------------------------
# CALCUL NON LINEAIRE
# --------------------------------------------------------------------
RESU=STAT_NON_LINE(MODELE=MOD,
CHAM_MATER=CHMAT,
EXCIT=(_F(CHARGE=BLOQ,),
_F(CHARGE=DEPL,
FONC_MULT=FONC,),
_F(CHARGE=CONT,),),
COMP_INCR=(_F(RELATION='ELAS',
DEFORMATION='PETIT_REAC',
GROUP_MA='VlSchi',),
_F(RELATION='ELAS',
DEFORMATION='PETIT_REAC',
GROUP_MA='VlRad',),),
INCREMENT=_F(LIST_INST=LINST,
SUBD_METHODE='UNIFORME',
SUBD_PAS=6,
SUBD_NIVEAU=5,
SUBD_PAS_MINI=1.0E-8,),
NEWTON=_F(MATRICE='TANGENTE',),
CONVERGENCE=_F(RESI_GLOB_RELA=1.0E-6,
ITER_GLOB_MAXI=300,),
SOLVEUR=_F(METHODE='MULT_FRONT',
SYME='OUI',),
INFO=1,);
#
# --------------------------------------------------------------------
# CALCUL DES CONTRAINTES AUX NOEUDS
# --------------------------------------------------------------------
#
RESU=CALC_ELEM(reuse =RESU,
MODELE=MOD,
CHAM_MATER=CHMAT,
RESULTAT=RESU,
OPTION=('SIEF_ELNO_ELGA','VARI_ELNO_ELGA','EQUI_ELNO_SIGM',),);
RESU=CALC_NO(reuse =RESU,
RESULTAT=RESU,
OPTION=('SIEF_NOEU_ELGA','VARI_NOEU_ELGA','EQUI_NOEU_SIGM',),);
RESU=CALC_NO(reuse =RESU,
RESULTAT=RESU,
OPTION='FORC_NODA',
MODELE=MOD,
CHAM_MATER=CHMAT,);
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Compute reaction force on the imposed displacement surface "DEPL"
# Caution : force expressed in n/radian
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
TAB_FORC=POST_RELEVE_T(ACTION=_F(OPERATION='EXTRACTION',
INTITULE='FORCE',
RESULTAT=RESU,
NOM_CHAM='FORC_NODA',
TOUT_ORDRE='OUI',
GROUP_NO='NDLoadA',
RESULTANTE='DY',),);
# Turn the table TAB_FORC into a function
FF=RECU_FONCTION(TABLE=TAB_FORC,
PARA_X='INST',
PARA_Y='DY',);
# Multiply the function by -1.
FY=CALC_FONCTION(COMB=_F(FONCTION=FF,
COEF=-1.,),);
# Create a function out of the displacement on node "Point"
DD=RECU_FONCTION(RESULTAT=RESU,
TOUT_ORDRE='OUI',
NOM_CHAM='DEPL',
NOM_CMP='DY',
GROUP_NO='NDLoadA',);
# Multiply the function by -1.
DY=CALC_FONCTION(COMB=_F(FONCTION=DD,
COEF=-1.,),);
# Print a nice postscript curve in 38 logic unit
IMPR_FONCTION(FORMAT='XMGRACE',
UNITE=28,
COURBE=_F(FONC_X=DY,
FONC_Y=FY,
COULEUR=2,),
SOUS_TITRE='Force (N/mm)',
LEGENDE_X='Depth (mm)',);
# Print text function in 39 logic unit
#IMPR_FONCTION(FORMAT='TABLEAU',
# COURBE=_F(FONC_X=DY,
# FONC_Y=FY,),
# UNITE=39,);
#
# --------------------------------------------------------------------
# CALCUL DES FORCES NODALES ET DES REACTIONS NODALES
# --------------------------------------------------------------------
#RESU=CALC_NO(reuse =RESU,
# RESULTAT=RESU,
# OPTION='REAC_NODA',
# MODELE=MOD,
# EXCIT=(_F(CHARGE=BLOQ,),
# _F(CHARGE=DEPL,
# FONC_MULT=FONC,),
# _F(CHARGE=LIAI,),
# _F(CHARGE=CONT,),),);
#
# =====================================================================
# Pro 21.01.09 GMSH OUTPUT
# FEHLER GMSH OUTPUT ENTFERNT DURCH EINSETZEN DER TERME FUER COMPOSANTES
# NOM_CMP=('SIXX','SIYY','SIXY',),),
# =====================================================================
IMPR_RESU(MODELE=MOD,
FORMAT='GMSH',
UNITE=81,
RESU=(_F(MAILLAGE=MAIL,
RESULTAT=RESU,
NOM_CHAM='DEPL',
NUME_ORDRE=4,),
_F(RESULTAT=RESU,
NOM_CHAM='SIEF_NOEU_ELGA',
NUME_ORDRE=4,
NOM_CMP=('SIXX','SIYY','SIZZ',),),
_F(RESULTAT=RESU,
NOM_CHAM='VARI_NOEU_ELGA',
NUME_ORDRE=4,),
_F(RESULTAT=RESU,
NOM_CHAM='EQUI_NOEU_SIGM',
NUME_ORDRE=4,
NOM_CMP=('PRIN_1','PRIN_2','PRIN_3','TRESCA',),),
_F(RESULTAT=RESU,
NOM_CHAM='VALE_CONT',
NUME_ORDRE=4,
NOM_CMP='RN',),),);
#
#IMPR_RESU(FORMAT='MED',
# UNITE=80,
# RESU=_F(MAILLAGE=MAIL,
# RESULTAT=RESU,
# NOM_CHAM=('DEPL','SIEF_NOEU_ELGA','VARI_NOEU_ELGA',),),);
# ===================
# STANLEY();
# ===================
# =====================================================================
FIN();
#
1) Knothe, K., Wille,
R. Zastrau, B.: Advanced Contact Mechanics - Road and Rail , International Journal
of Vehicle System Dynamics, 35(4-5), (2001), 361{407.
2) Nackenhorst, U.: Zur Berechnung schnell rollender Reifen mit der Finite Element Methode, Dissertation,
Universität der Bundeswehr Hamburg (1992) 3) Nackenhorst, U., Zastrau, B., Numerische Parameter
-studien zur Beanspruchung von Rad und Schiene beim Rollkontakt, EI-Eisenbahningenieur, 52(2), (2000), 48{52.
of Vehicle System Dynamics, 35(4-5), (2001), 361{407.
2) Nackenhorst, U.: Zur Berechnung schnell rollender Reifen mit der Finite Element Methode, Dissertation,
Universität der Bundeswehr Hamburg (1992) 3) Nackenhorst, U., Zastrau, B., Numerische Parameter
-studien zur Beanspruchung von Rad und Schiene beim Rollkontakt, EI-Eisenbahningenieur, 52(2), (2000), 48{52.